İtme ve momentum kavramları dinamik sorularını daha kolay çözebilmek için çıkarılmış kavramlardır. Dinamiğin temel yasası olan F=m.a bağıntısı geliştirilerek itme ve momentum denklemleri bulunabilir.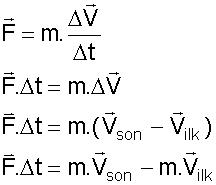
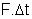 değerine itme denir ve I ile gösterilir. m.V değerine momentum denir ve P ile gösterilir. değerine itme denir ve I ile gösterilir. m.V değerine momentum denir ve P ile gösterilir.
Bu durumda yukarıda bulunan en son denklem şu şekilde ifade edilebilir:
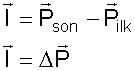
Yani bir cisme uygulanan itme o cismin momentumundaki değişime eşittir. Cismin son momentumundan ilk momentumunu çıkarırsak cisme uygulanan itmeyi buluruz. Momentum ve itme vektörel büyüklükler olduğundan bu çıkarma işlemi vektörel çıkarma olmalıdır.
MOMENTUMUN KORUNUMU
İki cismin çarpışmasında veya patlamalarda bileşke momentum değişmez. Yani kütle sisteminde bileşke kuvvet sıfır ise bileşke momentum değişmez.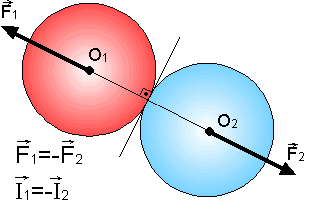
Yukarıdaki şekilde kırmızı ve mavi toplar çarpıştığı anda mavi topun kırmızı topa uyguladığı tepki kuvveti F1, kırmızının maviye uyguladığı F2 dir. Etki tepki kuvvetleri birbirine eşit büyüklükte ama zıt yönde olduğundan vektörel olarak F1=-F2 dir. Cisimlere uygulanan itmeler :
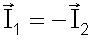
Çarpışma anındaki bu eşitlikten momentumun korunumunu ispatlayabiliriz:
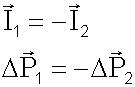
Bir cisme uygulanan itme o cismin momentum değişimine eşittir. Yani 1. cisme uygulanan itme 1. cismin momentum değişimine eşittir. Momentum deiğşimide Pson- Pilk olduğundan:
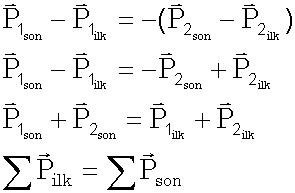
En son bulunan denklem çarpışmadan önceki ilk bileşke momentumun çarpışmadan sonraki son bileşke momentuma eşit olduğunu gösterir. Bu ilkeye momentumun korunumu ilkesi denir.
|