Maxwell Denklemleri
James Clerk Maxwell elektromanyetik dalgaları matematiksel olarak incelemek için bazı fiziksel büyüklükler kullanmıştır. Bu büyüklükler manyetik dolanım, elektriksel dolanım, manyetik akı, elektriksel akı, vb. dir. Bu büyüklüklerden bazılarını Lise2 konularından biliyorsunuz. İlkdefa göreceğiniz büyüklükler aşağıda tanımlanmıştır.
Elektriksel Dolanım (DE): Değişen bir manyetik alan etrafında birim yükü bir tur döndürmek için elektrik alana karşı yapılan iş.
Manyetik Dolanım (DB): Düz bir telden geçen akım veya değişken bir elektrik alan etrafında birim kuzey kutbunun bir tur dönmesi sırasında manyetik alana karşı yapılan iş.
ELEKRİKSEL DOLANIM
|
MANYETİK DOLANIM
|
|
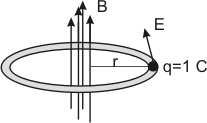
Bu resimde çembersel bir halkanın içinden geçen DEĞİŞKEN bir manyetik alan vardır. Bu manyetik alanın değişmesi çemberin manyetik akısını değiştirir. Değişen manyetik akı çemberden akım geçmesine neden olur. (elektromanyetik indüksiyon Lise2 konusu). Çembersel telden akım geçmesi demek, telin içinde elektrik alan oluşmasıyla açıklanır. Demekki tel olmasa bile, değişen manyetik alan etrafında elektrik alan çizgileri oluşur. Elektriksel dolanım birim yükün bir tur dolanması için elektriksel kuvvetlerin yaptığı iş olarak tanımlanır. Bu işi hesaplamak için, iş formülünde kuvvet yerine E, yol yerine 2π.r yazılırsa, DE=E.2π.r bulunur. Aynı zamanda bu tanım indüksiyon emk tanımıdır. İndüksiyon emk sı ise aşağdaki formülden bulunur.
|
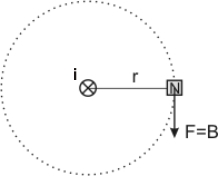
İş formülünün W=F.x olduğunu hatırlarsak, i akımı geçen düz bir tel etrafında birim kuzey kutbunu bir tur döndürmek için yapılan işi hesaplarız. Bu da bize manyetik dolanımı verir. DB=B.2π.r Çünkü birim kuzey kutbuna uygulanan kuvvet manyetik alan demektir. B=2Ki/r olacağından dolanım formulünde yerine yazılırsa, DB=2Ki/r.2π.r =4πKi bulunur.
Bu denklem akımın manyetik etkisi olarak tanımığımız bir denklemle yakından ilgilidir. B=2K.i/d
Yani şunu söylüyoruz: Akım geçen bir telin etrafında manyetik alan oluşur.
|
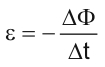 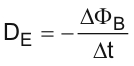 Bu formülden çıkan değer aynı zamanda elektrik dolanımı verir. Bu formülden çıkan değer aynı zamanda elektrik dolanımı verir.
Eşdeğer Akım
Şu ana kadar iki önemli denklem elde ettik. Bunlar manyetik dolanım (DB) ve elektriksel dolanımı (DE) veren formüller. Bunları aşağıdaki gibi yazabiliriz.
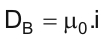 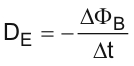
Manyetik dolanımın formülünden anlaşılacağı gibi, telden i büyüklüğünde bir akım geçtiğinde, bu akımı μ0 ile çarpmamız yeterli oluyor. μ0 sayısı boşluğun manyetik geçirgenliğidir. μ0 aynı zamanda 4π.K sayısına eşittir. (K sayısı manyetik alan konularından hatırlayacağınız 10-7 sayısıdır.)
Eğer ortamda bir i akımı yoksa, sanki akım varmış gibi bir etki yaratılıp, manyetik dolanım hesaplanabilir mi? Bu sorunun yanıtı için elektrik konularından hatırlayacağınız kondansatörleri inceleyelim. Kondansatör iki paralel levhadan oluşur ve akım geçtiğinde yüklenmeye başlar.
|
|
Şekildeki kondansatör başlangıçta nötrken, üretece bağlandığında, üreteçten akım geçer ve kondansatörün levhaları yüklenmeye başlar. Levhalar yüklendikçe kondansatörün levhaları arasındaki elektrik alan artar. Kondansatörle ilgili bildiğimiz denklemleri kullanarak elektrik alanın şiddetini veren formülü bulabiliriz.
Kondansatörün sığasını veren iki formül vardır.
|
| |
|
Kondansatörün levhaları arasında hava olduğundan buradan elektrik akımı geçmez. Yani levhalar arasından hiçbir zaman yük akışı olmaz. Fakat kondansatörün levhaları artı eksi yüklenirken tellerden akım geçer. Kondansatör tamamen dolduğunda ise tellerden geçen akım biter. Fakat hiçbir durumda levhalar arsındaki boşluktan akım geçmez.
Tellerden akım geçmekteyken (dolma aşamasında) levhalar arasında oluşan elektrik alan artar. Dolayısıyla kondansatörün elektriksel akısı artar. Tellerden akım geçmiyorken (kondansatör dolduktan sonra) elektrik alan sabit kalır yani zamanla değişmez.
"O halde elektriksel alan değişimi akım geçiyormuş etkisi yaratır. "
Bir ortamda elektriksel alan değişiyorsa, sanki orada elektrik akımı varmış gibi olur.
Bu kuralı manyetik dolanımda kullanalım. Bir telden akım geçtiğinde etrafında manyetik alan oluşuyordu. Akım yerine elektriksel alan değişimini koyabildiğimize göre, şunu söyleyebiliriz:
"Elektriksel alan değişimi etrafında manyetik alan yaratır."
Maxwel'in kurallarını şöyle özetleyebiliriz:
Değişen manyetik alanlar etrafında elektrik alanları, değişen elektrik alanlarda etrafında manyetik alanları oluşturur.
O halde bir ortamda değişen elektrik alan oluşturursak bu etrafında değişen manyetik alan oluşturacak, bu değişen manyetik alan da etrafında elektriksel alan oluturacak, bu tekrar manyetik alan ......................................
Bu şekilde elektrik ve manyetik alan değişimleri birbirini sürekli takip edecek. İşte elektro manyetik dalga böyle birbirini destekleyen elektrik ve manyetik alan değişimleridir.
|